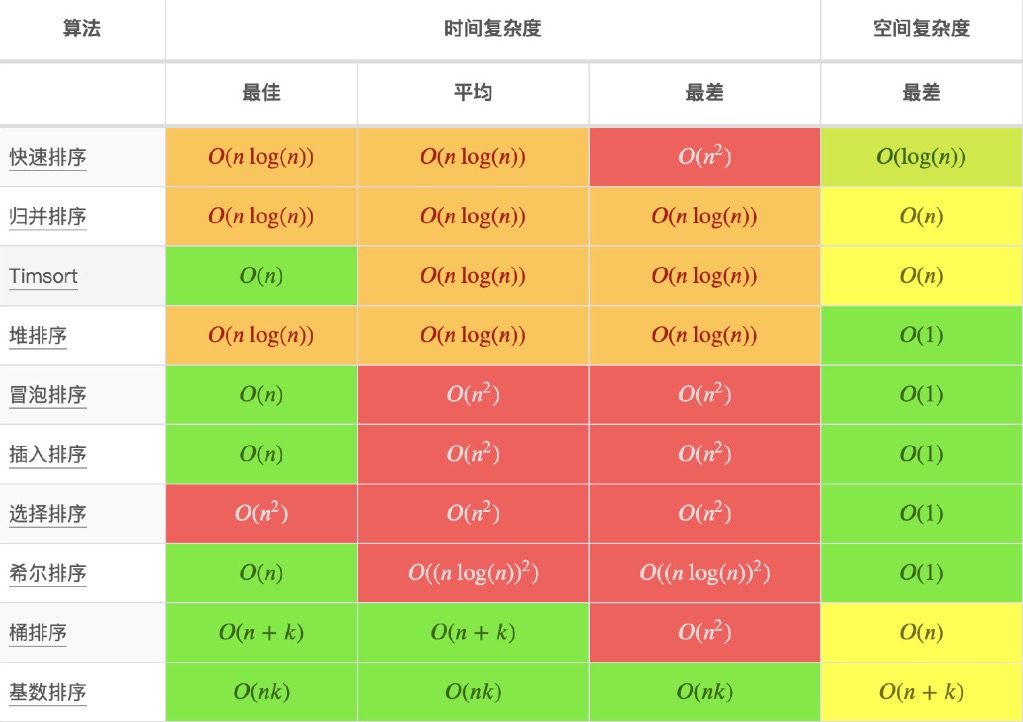
算法的时间复杂度 算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别。
那么我们应该如何去衡量不同算法之间的优劣呢?
主要还是从算法所占用的「时间」和「空间」两个维度去考量。
时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
上期我们学习了时间复杂度 ,下面我来分别介绍一下「空间复杂度」的计算方式。
常见的空间复杂度量级有:
常数空间复杂度 $ O(1) $
线性空间复杂度 $ O(n) $
对数空间复杂度 $ O(\log{N}) $
多项式空间复杂度 $ O(n^k) $
指数空间复杂度 $ O(n^2) $ 或 $ O(n^3) $
常数空间复杂度 $ O(1) $ 常数空间复杂度表示算法的内存使用是固定的,与输入规模无关。这通常意味着算法只使用了几个额外的变量或固定大小的数据结构,无论输入数据的大小如何,额外的内存占用都保持不变。
例如,一个反转数组的算法可以具有常数空间复杂度,因为它只需要一个或两个额外的变量来交换数组元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 #include <iostream> int sum_of_numbers (int n) int result = 0 ; for (int i = 1 ; i <= n; ++i) { result += i; } return result; } int main () int n = 5 ; int sum = sum_of_numbers (n); std::cout << "Sum of numbers from 1 to " << n << " is " << sum << std::endl; return 0 ; }
示例中,result 是唯一的额外变量,空间复杂度为 $ O(1) $ 。
线性空间复杂度 $ O(n) $ 线性空间复杂度表示算法的内存使用随着输入规模线性增长。这意味着算法需要一个与输入规模成正比的数据结构来存储或处理数据。
例如,合并排序算法通常具有线性空间复杂度,因为它需要额外的数组来合并和存储排序后的数据。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <iostream> #include <vector> int find_max_element (std::vector<int >& arr) int max_element = arr[0 ]; for (int i = 1 ; i < arr.size (); ++i) { if (arr[i] > max_element) { max_element = arr[i]; } } return max_element; } int main () std::vector<int > arr = {4 , 2 , 9 , 7 , 5 }; int max = find_max_element (arr); std::cout << "Max element in the array is " << max << std::endl; return 0 ; }
示例中,除了输入数组 arr 外,只有一个额外的变量 max_element,空间复杂度为 $ O(1) $ 。
对数空间复杂度 $ O(\log{N}) $ 对数空间复杂度表示算法的内存使用随着输入规模的对数增长。这通常出现在一些分治算法中,其中问题被递归地分割成较小的子问题,每个子问题只需要一部分额外的内存。
例如,二分查找算法具有对数空间复杂度,因为它只需要存储一个索引范围,而不需要额外存储每个元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> int binary_search (int arr[], int target, int left, int right) while (left <= right) { int mid = left + (right - left) / 2 ; if (arr[mid] == target) { return mid; } else if (arr[mid] < target) { left = mid + 1 ; } else { right = mid - 1 ; } } return -1 ; } int main () int arr[] = {1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 }; int target = 6 ; int index = binary_search (arr, target, 0 , sizeof (arr) / sizeof (arr[0 ]) - 1 ); if (index != -1 ) { std::cout << "Element " << target << " found at index " << index << std::endl; } else { std::cout << "Element not found" << std::endl; } return 0 ; }
多项式空间复杂度 $ O(n^k) $ 多项式空间复杂度表示算法的内存使用随着输入规模的某个多项式函数增长,其中k是一个常数。这通常出现在嵌套循环或多维数据结构的情况下。
例如,一个二维数组需要 $ O(n^2) $ 的内存来存储所有元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <iostream> #include <vector> std::vector<std::vector<int >> generate_matrix (int n) { std::vector<std::vector<int >> matrix (n, std::vector <int >(n, 0 )); int num = 1 ; for (int i = 0 ; i < n; ++i) { for (int j = 0 ; j < n; ++j) { matrix[i][j] = num++; } } return matrix; } int main () int n = 3 ; std::vector<std::vector<int >> result = generate_matrix (n); for (int i = 0 ; i < n; ++i) { for (int j = 0 ; j < n; ++j) { std::cout << result[i][j] << "\t" ; } std::cout << std::endl; } return 0 ; }
这个示例里,我们用一个二维矩阵 matrix ,大小为 n x n ,因此它的空间复杂度为 $ O(n^2) $ 。矩阵中的每个元素都会被初始化并赋值,然后最终输出矩阵。简单展示一下多项式空间复杂度的情况,其中空间需求随输入规模的平方增长。
指数空间复杂度 $ O(n^2) $ 或 $ O(n^3) $ 指数空间复杂度表示算法的内存使用随着输入规模的指数级增长。这是一种极端情况,通常不可接受,因为内存占用会迅速爆炸。
例如,某些穷举搜索算法可能具有指数空间复杂度,因为它们需要存储和遍历所有可能的组合。
总结 在分析算法的空间复杂度时,需要考虑以下因素:
额外数据结构: 算法是否需要额外的数据结构来存储中间结果或辅助计算?
递归调用: 递归算法可能会导致栈空间的额外消耗,这也需要考虑在内。
动态内存分配: 算法是否需要在运行时动态分配内存,例如,使用动态数组或链表?